Ch. 1 Structure of the Atom

Return to TOC

Atomic Discoveries Summarized

• Antoine Lavoisier: law of conservation of matter (1774)
• Joseph Proust: law of constant composition (1799)
• John Dalton: atomic theory (1803-1808)
  • law of multiple proportions
• Michael Faraday: electric current can cause chemical reactions (1834)
• Sir William Crooks: cathode ray tube (1870s)
• J.J. Thomson: charge to mass ratio (1897)
  • plum pudding model
• Robert Millikan: oil drop experiment (1909)
• Ernest Rutherford: gold foil experiment
  • nuclear model
  • proton (1919)
• Niels Bohr: solar system model (1913)
• Erwin Schrödinger: wave-mechanical theory (1927)
• Werner Heisenberg: uncertainty principle (1920s)

Name	Symbol	Charge (Coulombs)	Mass
Electron	$e$ or $e^-$	$- 1.602 \cdot 10^{- 19}$ (-1)	$9.109 \cdot 10^{- 28}$ ($5.486 \cdot 10^{- 4}$)
Proton	$p$	$1.602 \cdot 10^{- 19}$ (+1)	$1.673 \cdot 10^{- 24}$ (1.0073)
Neutron	$n$	0	$1.675 \cdot 10^{- 25}$ (1.0087)

---

Electromagnetic Spectrum

---

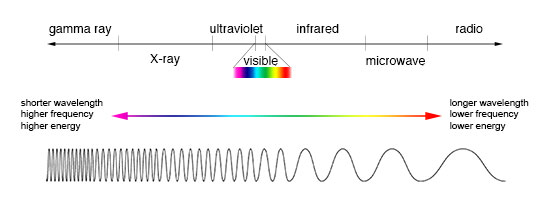
Light

$($Wavelength$)($Frequency$)=($Speed of Light$)$
$\textcolor{#EE4266}{\lambda} \textcolor{#F79256}{v}=\textcolor{yellow}{c}=299,792,458\text{ m/s}\approx 3.0\cdot10^8\text{ m/s}$
$($Energy$)=($Planck's constant$)($Frequency$)$
$E=\textcolor{lightblue}{h}\textcolor{#F79256}{v}=\textcolor{lightblue}{h}\frac{\textcolor{yellow}{c}}{\textcolor{#EE4266}{\lambda}}=mc^2,\textcolor{lightblue}{h}=$$6.63 \cdot 10^{- 34} \text{ J} \cdot \text{s}$

Example Problem

Find the frequency and energy of 400. nm light
$\lambda = 400 . \text{ nm}$
$\left( 400 . \text{ nm} \right ) v = 3.0 \cdot 10^{8} \text{ m s}^{- 1}$
$v = \frac{3.0 \cdot 10^{8} \text{ m s}^{- 1}}{4.00 \cdot 10^{- 7} \text{ m}} = 7.5 \cdot 10^{14} \text{ s}^{- 1}$
$E = h v = \left( 6.63 \cdot 10^{- 34} \text{ J s} \right ) \left( 7.5 \cdot 10^{14} \text{ s}^{- 1} \right ) = 5.0 \cdot 10^{- 19} \text{ J}$

---

Energy in a orbital (principal quantum number) $n$: $E_{n} = \frac{- 2 \pi^{2} m e^{4}}{n^{2} h^{2}} = \frac{- 2.178 \cdot 10^{- 18}}{n^{2}} \text{ J}$

---

Energy Levels

Principal Energy Levels (Shells): 1, 2, 3, 4,...
Sublevels (Subshells): s, p, d, f
Orbitals: 1, 3, 5, 7 pairs of $e^-$ can fit in sublevel

---

Electrons

Electron Configuration: e.g. $1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 4 s^{2} 3 d^{10} \ldots$ or abbreviated

Electron Configuration for $\ce{Fe}$

$\ce{Fe}=1s^2 2s^2 2p^6 3s^2 3p^6 4s^2 3d^6$
$\ce{Fe}=[\ce{Ar}] 4s^2 3d^6$

Valence Electrons: Outside electrons; sum of s and p orbitals
Hund's Rule: p, d, and f orbitals must have one electron in each orbital before they can pair up